| • About MotCo • Features • Downloads • Tutorials |
• Data • References • Recommendations and participation • Contacts |

The aim of the project is to apply a hierarchical genetic algorithm (HGA) for investigation of human limbs motions. HGA is capable of modelling natural hierarchy in brain control mechanisms. It is also suitable means for studying the process of training and learning. In contrast to other scientific approaches for motor control investigation, such as static and dynamic optimization, or using of Hill’ type muscle models, here, the mechanical output of a muscle is not represented as one single force, but as a mixture of motor units (MUs) with different peculiarities. Similarly to natural muscular systems, firing rates of MUs are subjects to control from HGA and to genetic operations. The aim of the control is modelled by a fitness function that is a weighted combination from different optimization criteria such as: precise tracing of the joint moments, minimal sum of muscle forces, minimal activation, minimal fatigue, etc. In this way movements with different aims could be modeled. Unlike to artificial neural networks, HGA is not a “black box” method, it resembles the natural way for achievement the desired movement by using time dependent, multi-objective criteria. Its future development will help in better understanding of human motor control. The possibilities for further applications in medicine and sport biomechanics are very wide and promising.
The Main Idea
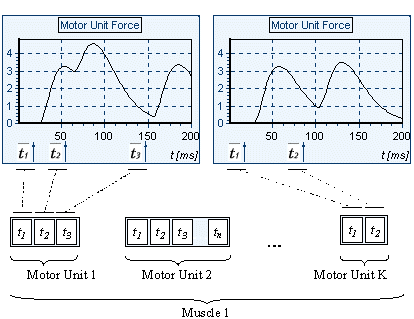
The smallest part of a muscle controlled by nervous system, hence the smallest force generator, is the motor unit (MU). A MU consists of muscle fibers innervated by a motoneuron. The mechanical response of a MU to one single neural stimulus is called “twitch”. The form of the twitch is different for different MUs types (fast, slow, intermediate). Depending on the neural stimulation applied to a MU, it develops a force that is formed by a superimposition of these twitches. The sum of the forces of all MUs constituting a muscle is the force of this muscle. The moments of the forces of all modeled muscles cause rotations in the joints, and in consequence the end link of the limb moves in the space. The general aim of the program is: giving a particular movement to find the activation of all MUs of all modelled muscles so that the forces of these muscles are able to perform the movement and to satisfy the imposed goals. The movement can be defined as: time dependencies of joint angles; trajectories of the end point and rotation centers of the joints or start and end position of the links (reaching task); support of a position for a fixed time without or with external disturbance, without or with muscle fatigue, etc.
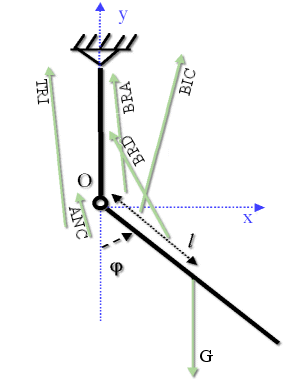
Muscle-Joint-Bone System
The links of models are considered rigid bodies, their mass-inertial characteristics and dimensions are considered known parameters. The links are connected by rotation frictionless joins with 1, 2 or 3 degrees of freedom (DOF). Freedom of the movement in the joints is limited by maximal and minimal anatomical admissible values of the angle displacement. The whole muscle is determined by its attachment points, dependencies of the its lever arms with respect to different axis of rotation (depending on the considered DOF) from joint angles, physiological cross-sectional area and optimal length. On the lower level of hierarchy the muscle consists of different types MUs.
Motor Units
The shape of the developed force of a MU due to a single neural stimulus, i.e. its twitch, can be described analytically by the following constants (see the figure in Feature toolbox):
- FMUmax – maximal force;
- Tlead – “lead time”: the time between neural stimulation and beginning of the force development;
- Tc – “contraction time’: time from the start of the MU’mechanical contraction to the time where MU force reaches its maximum;
- Tref – “absolute refractory period”: during this time the MU is unable to respond to new neural stimulation;
- Thr – “half-relaxation time”: time from the start of the MU mechanical responce to the time when the MU force becomes twice lower than FMUmax;
- Ttw – duration of the twitch.
Depending on the values of these constants four type MUs are distinguished:
- I – fast twitch-fatigue resistant (FR);
- II – fast twitch-fatiguable (FF);
- III – intermediate (IM);
- IV – slow twitch (S).
Independently of these default values, everyone may choose these constants thus defining other types of MUs. A parameter that accounts for MUs fatigue during prolonged motor activity is also provided. It is defined as a non-linear decrease of FMUmax depending on the MU activity during the preceding time period.
Hierarchical genetic algorithm
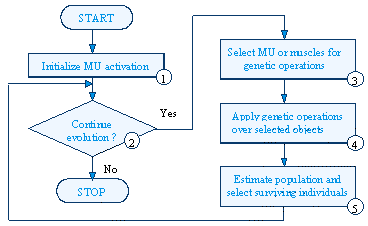
Classical Genetic Algorithm (GA) is inspired by natural evolution where the fittest individuals survive. GA presumes that the potential solution of any problem is an “individual” and can be represented by set of parameters. These parameters are regarded as genes of a chromosome and can be structured by string of values. On each step of the algorithm a subsequent generation is created by means of genetic operations (mutation and crossover). In this process of evolution the “better” chromosomes generate a larger number of offspring, and thus have a higher chance of surviving. In HGA, besides the regular genes there are control genes also. The control genes activate or inhibit a given subset of regular genes.
In the present model genes encode the time moments of neural stimulation of the associated motor units. Therefore each “individual”, obtained by a concatenation of the strings associated with MUs, represents the overall activity of the muscle system. This activity is modified by mutation operations or is combined from two different solutions by crossover operations. Thus new solutions are obtained and they together with the previous ones are evaluated by a fitness function. The fitness function is a combination of functions that estimate the “goodness” of the individuals with respect to different criteria (minimal total muscle force, minimal muscle fatigue, maximal trajectory accuracy, etc.)
Current results
Only elbow joint is modeled so far. Flexion and extension movements with different duration and initial and final positions are investigated. The main flexor and extensor muscles are considered in the model: BIC (m.biceps brachii), BRA (m.brachialis), BRD (m.brachioradialis), TRI (m.triceps brachii), ANC (m.anconeus). Their lever arms with respect to the rotation center in the elbow joint are supposed dependent on the joint angle and regression equations are used for their calculations. The following optimization criteria are realized and tested:
- minimal sum of all muscle forces;
- minimal MUs activation;
- minimal MUs fatigue;
- minimal sum of the muscle stresses (muscle forces divided to the muscle physiological cross-sectional area);
- minimal total error between desired and actual (calculated) elbow joint moment.
All these criteria can be combined with different weights in a fitness function. Most of the simulations were performed using less than actual number of MUs, because of very fast increase of the computational load with the increase of the total number of the MUs considered in the model. Very fast elbow flexion (from 0 to 150 degrees for 200 ms) is investigated using nearly real number of MUs: m.BIC – 774 MUs, m.BRA – 804 MUs, m.BRD – 194 MUs, m.TRI – 686 MUs, m.ANC – 180 MUs. The influence of the relation between the number of fast and slow MUs on the predicted muscle forces and so called “simulated EMG” (the number of applied neural impulses for a given time period) is investigated.